ARPL

Adversarially Robust Policy Learning: Active Construction of Physically-Plausible Perturbations

Abstract

Policy search methods in reinforcement learning have demonstrated success in scaling up to larger problems beyond toy examples. However, deploying these methods on real robots remains challenging due to the large sample complexity required during learning and their vulnerability to malicious intervention. We introduce Adversarially Robust Policy Learning (ARPL), an algorithm that leverages active computation of physically-plausible adversarial examples during training to enable robust policy learning in the source domain and robust performance under both random and adversarial input perturbations. We evaluate ARPL on four continuous control tasks and show superior resilience to changes in physical environment dynamics parameters and environment state as compared to state-of-the-art robust policy learning methods.

Methods

We work with a physical dynamical system model:

\[ s_{t+1} = f(s_t, a_t; \mu) + \nu \]

\[ o_t = g(s_t) + \omega \]

Here, \(x_t\) denotes the state of the system at time \(t\), \(a_t\) denotes the control, or action, applied at time \(t\), \(f\) models the transition function (dynamics) of the system, \(\mu\) parametrizes \(f\), \(\nu\) models process noise, \(g\) models the observation function of the system, and \(\omega\) denotes observation noise. We introduce adversarial perturbations to 3 key components of this system - perturbations in the dynamics (\(\mu\)), the process (\(\nu\)), and the observation (\(\omega\)).

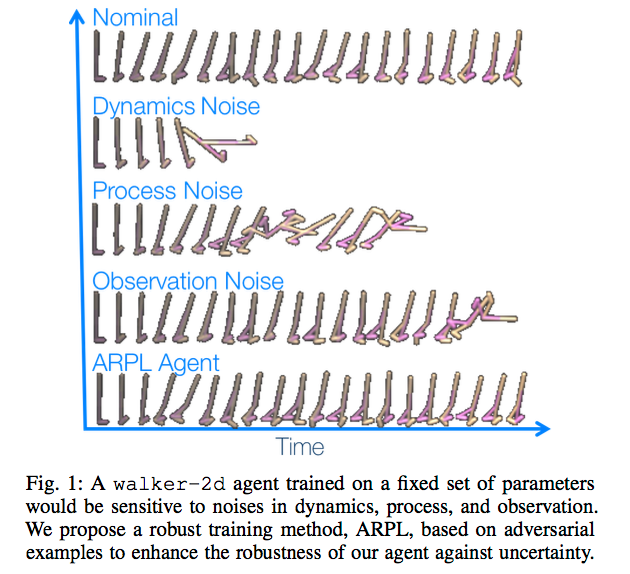
We refer to these respectively as dynamics noise, process noise, and observation noise. Dynamics noise refers to a perturbation in underlying system parameters such as mass or friction, while process noise and observation noise relate to direct perturbation of the state and observation. In order to produce these perturbations, we use a scaled version of the gradient of the loss function with respect to the state that the agent observes. This is easily achieved via backpropagation in the policy network.

We investigate the effects of these 3 different types of noise in 4 Mujoco environments under different frequencies of perturbation during both train time and test time, and under both random and adversarial generation.

Results

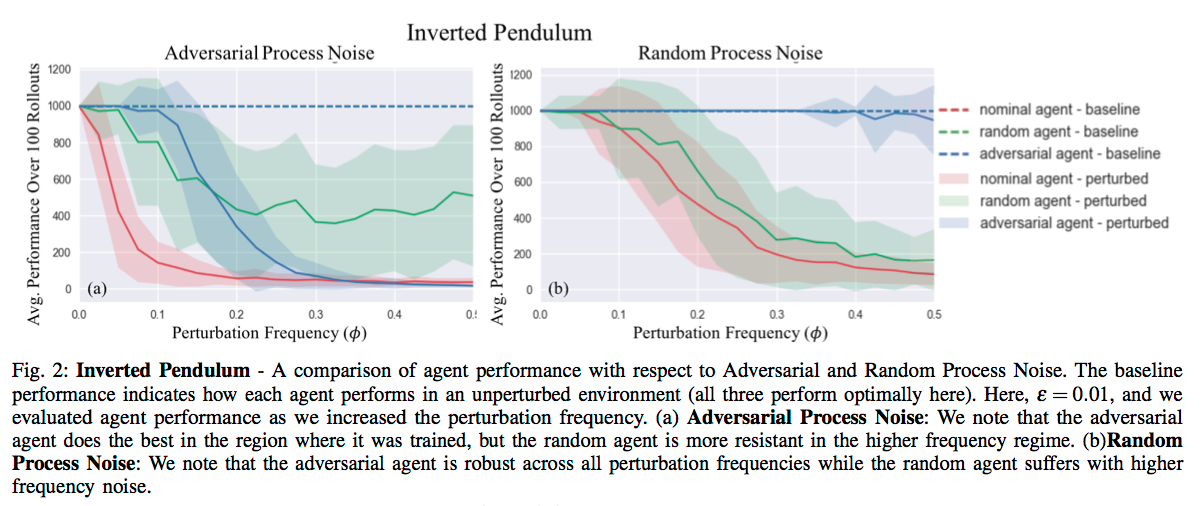
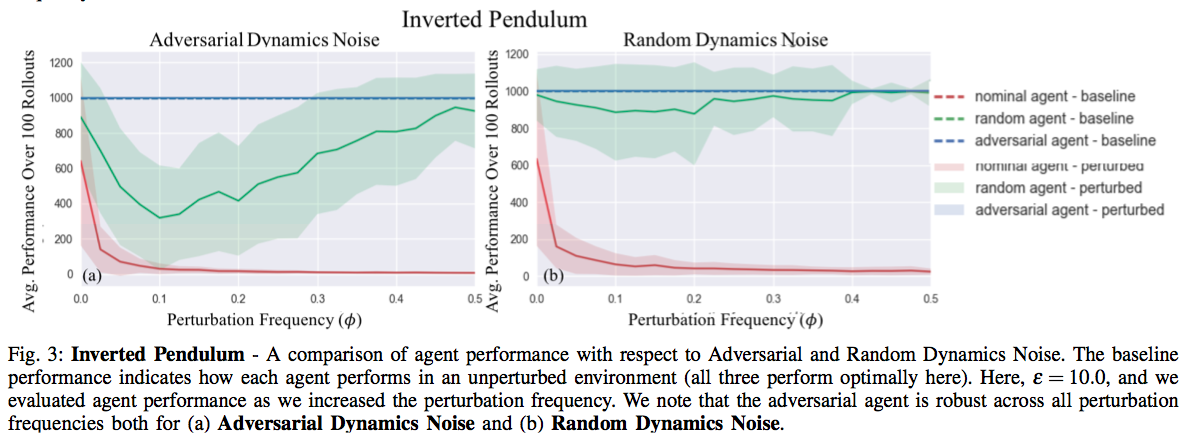
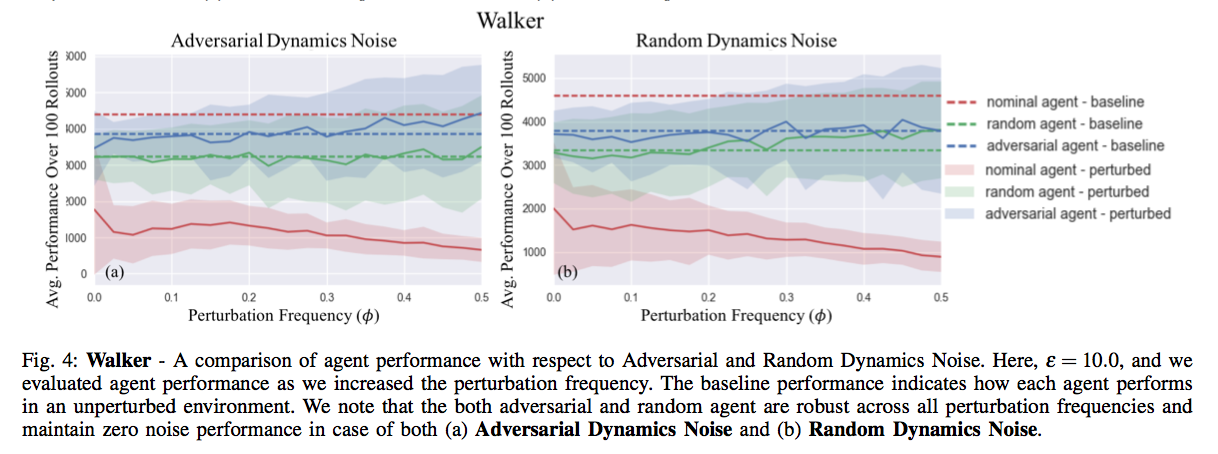
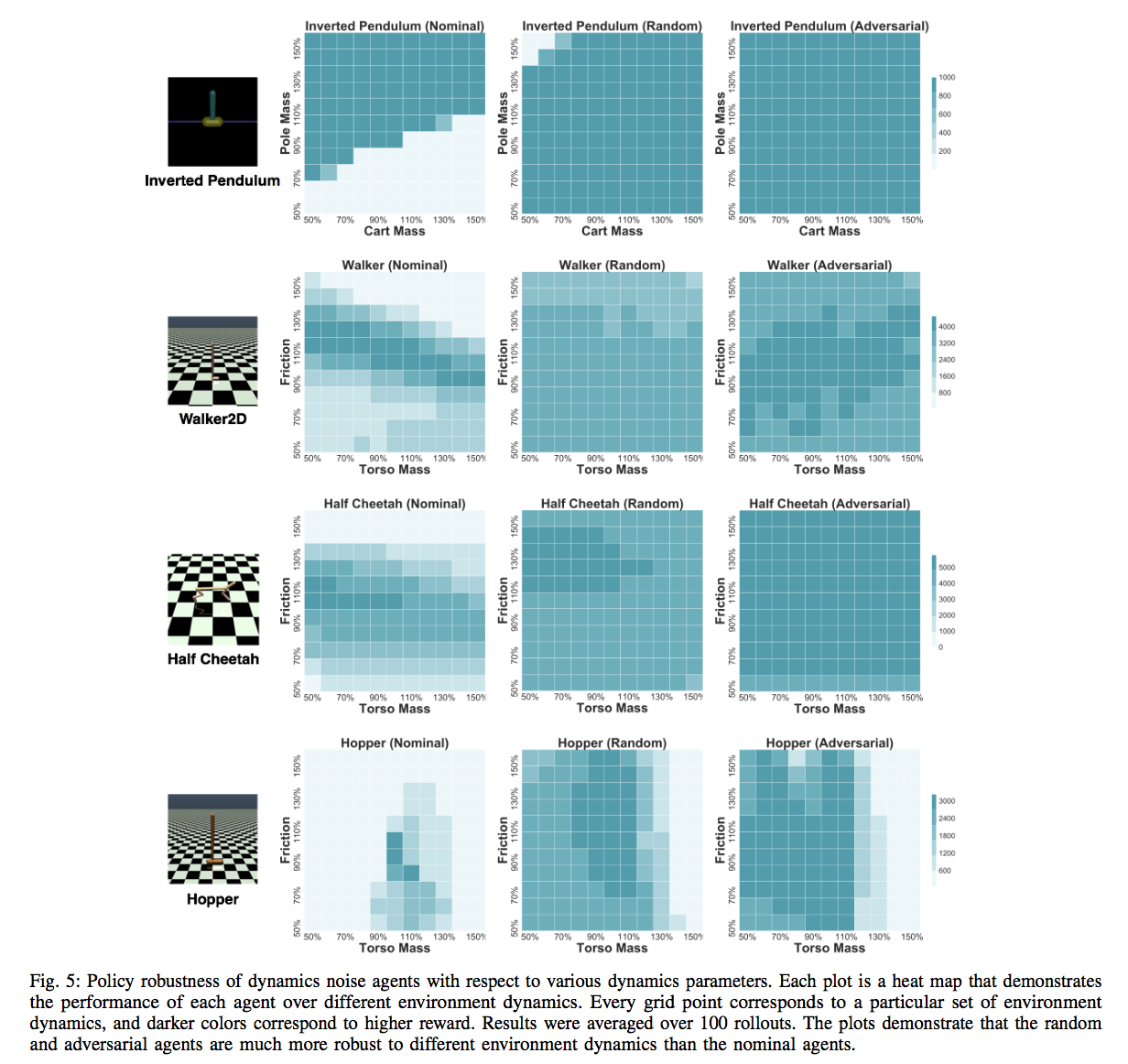
References

• Adversarially Robust Policy Learning: Active Construction of Physically-Plausible Perturbations.
  Ajay Mandlekar*, Yuke Zhu*, Animesh Garg*, Li Fei-Fei, Silvio Savarese (* denotes equal contribution).
  IEEE International Conference on Intelligent Robotics and Systems, (IROS) 2017

Authors and Contributors

Ajay Mandlekar, Yuke Zhu, Animesh Garg
PIs: Fei-Fei Li, Silvio Savarese

Support or Contact

Please Contact Animesh Garg at garg@cs.stanford.edu